Word2Vec知识简述

背景

谷歌2013年提出的Word2Vec是目前最常用的词嵌入模型之一。Word2Vec实际是一种浅层的神经网络模型，它有两种网络结构，分别是CBOW（Continues Bag of Words）和Skip-gram。

负采样（Negative Sample）和层次softmax（Hierarchical Softmax）则是两种加速训练的方法。

工作流程

CBOW的目标是根据上下文出现的词语来预测当前词的生成概率；而Skip-gram是根据当前词来预测上下文中各词的生成概率。

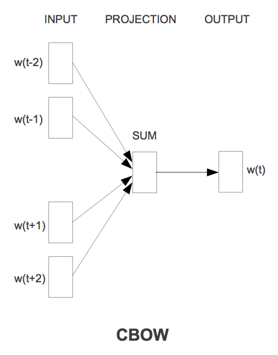
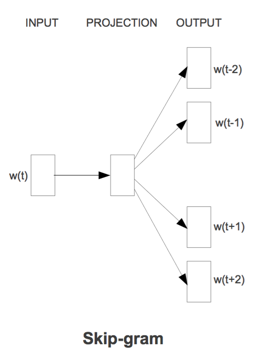
其中$w(t)$是当前所关注的词，$w(t-2)、w(t-1)、w(t+1)、w(t+2)$是上下文中出现的词。这里前后滑动窗口大小均设为2。

CBOW和Skip-gram都可以表示成由输入层（Input）、映射层（Projection）和输出层（Output）组成的神经网络。

输入层中的每个词由独热编码方式表示，即所有词均表示成一个N维向量，其中N为词汇表中单词的总数。在向量中，每个词都将与之对应的维度置为1，其余维度的值均设为0。

在映射层（又称隐含层）中，K个隐含单元（Hidden Units）的取值可以由N维输入向量以及连接输入和隐含单元之间的N*K维权重矩阵计算得到。在CBOW中，还需要将各个输入词所计算出的隐含单元求和。

同理，输出层向量的值可以通过隐含层向量（K维），以及连接隐含层和输出层之间的K*N维权重矩阵计算得到。输出层也是一个N维向量，每维与词汇表中的一个单词相对应。最后，对输出层向量应用softmax激活函数，可以计算出每个单词的生成概率。Softmax函数定义为：

$$p(y=w_n|x) = \frac{e^{x_{n}}}{\sum_{k=1}^{N}e^{x_{k}}}$$

其中$x$代表N维的原始输出向量，$x_n$为在原始输出向量中，与单词$w_n$所对应维度的取值。

接下来的任务就是训练神经网络的权重，使得语料库中所有单词的整体生成概率最大化。从输入层到隐含层需要一个维度为N*K的权重矩阵，从隐含层到输入层需要一个维度K*N的权重矩阵，学习权重可以用反向传播算法实现。但由于Softmax中存在归一化项的缘故，推导出的迭代公式需要对词汇表中的所有单词进行遍历，使得每次迭代过程非常缓慢，因此需要改进。最终训练得到维度为N*K和K*N的两个权重矩阵之后，可以选择其中一个作为N个词的K维向量表示。

负采样

最后的softmax分出来的类是整个词袋的大小，那么是不是可以把词袋大小减小，因为有些出现概率低的词我们根本可以不考虑。这就是负采样的核心思想。

假设我们有一个训练样本，中心词是$w$，它周围上下文共有$2c$个词，记为$context(w)$。由于这个中心词$w$的确和$content(w)$相关存在，因此它是一个真实的正例。通过Negative Sampling 采样，得到n个和$w$不同的中心词$w_i,i =1,2,…,n$，这样$context(w)$和$w_i$就组成了n个并不存在的负例。利用这一个正例和n个负例，进行二元逻辑回归，得到负采样对应的每个词$w_i$对应的模型参数$\theta_i$和每个词的词向量。整个过程相比Hierarchical Softmax简单。

但需要明确两个问题：（1）如何通过一个正例和n个负例进行二元逻辑回归？（2）如何进行负采样？

梯度计算

这里我们将正例定义为$w_0$。

在逻辑回归中，正例期望满足：

$$P(context(w_0),w_i)=\sigma(x_{w_0}^T\theta^{w_i}),y_i=1,i=0$$

负期望满足：

$$P(context(w_0),w_i)=1-\sigma(x_{w_0}^T\theta^{w_i}),y_i=0,i=1,2,..n$$

其对应的对数似然函数为：

$$L= \sum_{i=0}^ny_ilog(\sigma(x_{w_0}^T\theta^{w_i}))+(1-y_i)log(1-\sigma(x_{w_0}^T\theta^{w_i}))$$

和层次Softmax类似，采用随机梯度上升法，仅仅每次只用一个样本更新梯度，来进行迭代更新得到我们需要的$x_{w_i},\theta^{w_i}$。求导得梯度表达式，用梯度上升法进行一步步的求解。

负采样方法

word2vec采用的方法不复杂，如果词汇表的大小为V，那么我们就将一段长度为1的线段分成V份，每份对应词汇表中的一个词。当然每个词对应的线段长度是不一样的，高频词对应的线段长，低频词对应的线段短，每个词$w$的线段长度由下式决定：

$$len(w) =\frac{count(w)}{\sum_{\mu\in vocab}count(\mu)}$$

在word2vec中，分子和分母都取了3/4次幂如下：

$$len(w) =\frac{count(w)^{3/4}}{\sum_{\mu\in vocab}count(\mu)^{3/4}}$$

　在采样前，我们将这段长度为1的线段划分成$M$等份，这里$M>>V$，这样可以保证每个词对应的线段都会划分成对应的小块。而M份中的每一份都会落在某一个词对应的线段上。在采样的时候，我们只需要从$M$个位置中采样出$n$个位置就行，此时采样到的每一个位置对应到的线段所属的词就是我们的负例词。

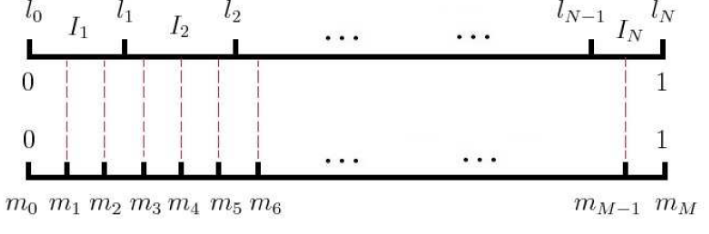
在word2vec中，$M$取值默认为$10^8$

层次softmax

Hierarchical Softmax，层次softmax是一种加速训练的技巧，要解决的问题是原来softmax的参数太多的问题，所以不管是层次softmax也好，还是负采样也好，都是对最后的softmax做一个处理。

层次softmax的核心内容是哈夫曼树（Huffman Tree）。树的核心概念是 出现概率越高的符号使用较短的编码（层次越浅），出现概率低的符号则使用较长的编码（层次越深）。

缺点

使用霍夫曼树来替代传统的神经网络，可以提高模型训练的效率。但是如果我们的训练样本里的中心词$w$是一个很生僻的词，那么就得在霍夫曼树中辛苦的向下走很久了。负采样比之而言考虑了该问题，不再使用霍夫曼树。

参考资料

• 《百面机器学习》
• word2vector的原理，结构，训练过程
• word2vec原理