主题模型产生背景
基于词袋模型或N-gram模型的文本表示模型有一个明显的缺陷,就是无法识别出两个不同的词或词组具有相同的主题。因此,需要一种技术能够将具有相同主题的词或词组映射到同一维度上去,于是产生了主题模型。
假设有K个主题,我们就把任意文章表示成一个K维的主题向量,其中向量的每一维代表一个主题,权重代表这篇文章属于这个特定主题的概率。主题模型所解决的事情,就是从文本库中发现有代表性的主题(得到每个主题上面词的分布),并且计算出每篇文章对应着哪些主题。
常见的主题模型
pLSA (Probabilistic Latent Semantic Analysis)
pLSA是用一个生成模型来建模文章的生成过程,增加了主题模型,形成简单的贝叶斯网络,可以使用EM算法学习模型参数。
pLSA图模型如下图所示:

假设有K个主题,M篇文章;对语料库中的任意文章d,假设该文章有N个词,则对于其中的每一个词,我们首先选择一个主题z,然后在当前主题的基础上生成一个词w。
(1)D代表文档,Z代表主题(隐含类别),W代表单词;$P(d_i)$表示文档$d_i$的出现概率,$P(z_k|d_i)$表示文档$d_i$中主题$z_k$的出现概率,$P(w_j|z_k)$表示给定主题$z_k$出现单词$w_j$的概率。
(2)每个主题在所有词项上服从多项分布,每个文档在所有主题上服从多项分布。
(3)给定文章d,生成词w的概率可以表示为:
这里我们做一个简化,假设给定主题z的条件下,生成词w的概率是与特定的文章无关的,则公式可以简化为:
(4)整个语料库中的文本生成概率可以用似然函数表示为:
其中$p(d_m,w_n)$是在第m篇文章$d_m$中,出现单词$w_n$的概率,即联合概率分布;$c(d_m,w_m)$是在第m篇文章$d_m$中,单词$w_n$出现的次数。利用对数似然简化计算得:
在上面的公式中,定义在文章上的主题分布$p(z_k|d_m)$和定义在主题上的词分布$p(w_n|z_k)$是待估计的参数。由于参数中包含的$z_k$是隐含变量(即无法直接观测到的变量),因此无法利用最大似然估计直接求解,可以利用最大期望算法(EM)来解决。
(5)EM算法的求解过程
需要求解隐变量$z_k$的后验概率,目标函数建立将约束问题求解使用Lagrange乘子法处理。
关于EM算法迭代如下:
M-step:
E-step:
(6)pLSA总结
- pLSA应用于信息检索、过滤、自然语言处理等领域,pLSA考虑到词分布和主题分布,使用EM算法来学习参数。
- 虽然推导略显复杂,但最终公式简洁清晰,很符合直观理解,需用心琢磨;此外,推导过程使用了EM算法,也是学习EM算法的重要素材。
LDA
LDA可以看作是pLSA的贝叶斯版本,其文本生成过程与pLSA基本相同,不同的是为主题分布分别加了两个狄利克雷(Dirichlet)先验。
为什么要加入狄利克雷先验呢?pLSA采用的是频率派思想,将每篇文章对应的主题分布$p(z_k|d_m)$和每个主题对应的词分布$p(w_n|z_k)$看作确定的未知常数,并可以求解出来;而LDA采用的是贝叶斯学派的思想,认为待估计的参数(主题分布和词分布)不再是一个固定的常数,而是服从一定分布的随机变量。这个分布符合一定的先验概率分布(即狄利克雷分布),并且在观察到样本信息之后,可以对先验分布进行修正,从而得到后验分布。LDA之所以选择狄利克雷分布作为先验分布,是因为它为多项式分布的共轭先验概率分布,后验概率依然服从狄利克雷分布,这样做可以为计算带来便利。下图为LDA的图模型,其中$\alpha,\beta$分别为两个狄利克雷分布的超参数,为人工设定。图中m为文章数,K为主题数,n表示文章的第n个词。
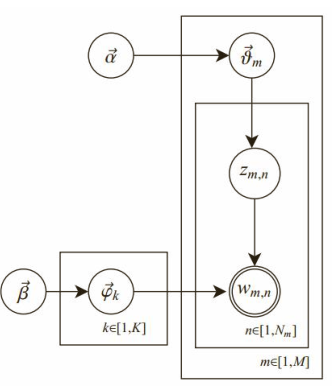
语料库的生成过程为:对文本库中的每一篇文档$d_i$,采用以下操作:
(1)从超参数为$\alpha$的狄利克雷分布中抽样生成文档$d_i$的主题分布$\theta_i$。
(2)对文档$d_i$中的每一个词进行以下3个操作。
- 从代表主题的多项式分布$\thetai$中抽样生成它所对应的主题$z{i,j}$。
- 从超参数为$\beta$的狄利克雷分布中抽样生成主题$z{i,j}$对应的词分布$\psi{z_{i,j}}$。
- 从代表词的多项式分布$\psi{z{i,j}}$中抽样生成词$w_{i,j}$。
求解主题分布$\thetai$以及词分布$\psi{z_{i,j}}$的期望,可以用吉布斯采样(Gibbs Sampling)的方式实现。
首先随机给定每个单词的主题,然后在其他变量固定的情况下,根据转移概率抽样生成每个单词的新主题。对于每个单词来说,转移概率可以理解为:给定文章中的所有单词以及除自身以外其他所有单词的主题,在此条件下该单词对应为各个新主题的概率。最后,经过反复迭代,我们可以根据收敛后的采样结果计算主题分布和词分布的期望。
如何确定LDA模型中的主题个数
在LDA中,主题的个数K是一个预先指定的超参数。对于模型超参数的选择,实践中的做法一般是将全部数据集分为训练集、验证集和测试集三个部分,然后利用验证集对超参数进行选择。
为了衡量LDA模型在验证集和测试集上的效果,需要寻找一个合适的评估指标。一个常用的评估指标是困惑度(perplexity)。在文档集合D上,模型的困惑度被定义为:
其中M为文档的总数,$w_d$为文档d中单词所组成的词袋向量,$p(w_d)$为模型所预测的文档d的生成概率,$N_d$为文档d中单词的总数。
一开始,随着主题数的增多,模型在训练集和验证集的困惑度呈下降趋势,但当主题数目足够大的时候,会出现过拟合,导致困惑度指标在训练集上继续下降但在验证集上反而增长。这时可以取验证集的困惑度极小值点可能出现在主题数目非常大的时候,然而实际应用并不能承受如此大的主题数目,这时需要在实际应用中合理的主题数目范围内进行选择,比如选择合理范围内困惑度的下降明显变慢(拐点)的时候。
另一种方法是在LDA基础上融入分层狄利克雷过程(Hierarchical Dirichlet Process,HDP),构成一种非参数主题模型HDP-LDA。非参数主题模型的好处是不需要预先指定主题的个数,模型可以随着文档数目的变化而自动对主题个数进行调整;它的缺点是在LDA基础上融入HDP之后使得整个概率图模型更加复杂,训练速度也更加缓慢,因此在实际应用中还是经常采用第一种方法确定合适的主题数目。

