知识背景
马尔可夫链
马尔可夫过程是满足无后效性的随机过程。假设一个随机过程中,$tn$时刻的状态$x_n$的条件分布,仅仅与其前一个状态$x{n-1}$有关,即$P(xn|x_1,x_2,…x{n-1})=P(xn|x{n-1})$,则将其称为马尔可夫过程,时间和状态的取值都是离散的马尔可夫过程也称为马尔可夫链。
隐马尔可夫模型(HMM)
隐马尔可夫模型是对含有未知参数(隐状态)的马尔可夫链进行建模的生成模型,概率图模型如下图所示。
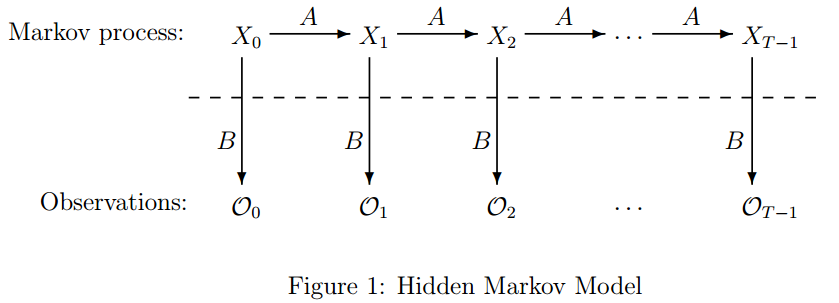
在简单的马尔可夫模型中,所有状态对于观测者都是可见的,因此在马尔可夫模型中仅仅包括状态间的转移概率。而在隐马尔可夫模型中,隐状态$x_i$对于观测者而言是不可见的,观测者能观测到的只有每个隐状态$x_i$对应的输出$o_i$,而观测状态$o_i$的概率分布仅仅取决于对应的隐状态$x_i$。在隐马尔可夫模型中,参数包含了隐状态间的转移概率、隐状态到观测状态的输出概率、隐状态$x$的取值空间、观测状态$o$的取值空间以及初始状态的概率分布。
隐马尔可夫模型三个基本问题与相应的算法
前向、后向算法解决的是评估问题,即给定一个模型,求某特定观测序列的概率,用于评估该序列最匹配的模型。(概率计算问题)
Baum-Welch算法解决的是模型训练问题,求解使得该观测序列概率最大的模型参数,即参数估计,是一种无监督的训练方法,主要通过EM迭代实现。(学习问题)
维特比(Viterbi)算法解决的是给定一个模型和某个特定的输出序列,求最可能产生这个输出的状态序列。例如,通过海藻变化(输出序列)来观测天气(状态序列),是预测问题,通信中的解码问题。
隐马尔可夫对中文分词问题建模与训练
例如有3个不同的葫芦,每个葫芦里有好药和坏药若干,现在从3个葫芦中按照以下规则倒出药来。
(1)随机挑选一个葫芦。
(2)从葫芦里倒出一颗药,记录是好药还是坏药后将药放回。
(3)从当前葫芦依照一定的概率转移到下一个葫芦。
(4)重复步骤(2)和(3)。
在整个过程中,我们并不知道每次拿到得是哪一个葫芦。用隐马尔可夫模型来描述以上过程,隐状态就是当前是哪一个葫芦,隐状态的取值空间为{葫芦1,葫芦2,葫芦3},观测状态的取值空间为{好药,坏药},初始状态的概率分布就是第(1)步随机挑选葫芦的概率分布,隐状态间的转移概率就是从当前葫芦转移到下一个葫芦的概率,而隐状态到观测状态的输出概率就是每个葫芦里好药和坏药的概率。记录下来药的顺序就是观测状态的序列,而每次拿到的葫芦的顺序就是隐状态的序列。
隐马尔可夫模型通常用来解决序列标注问题,因此也可以将分词问题转化为一个序列标注问题来进行建模。例如可以对中文句子中每个字做以下标注:B表示一个词开头的第一个字,E表示一个词结尾的最后一个字,M表示一个词中间的字,S表示一个单字词,则隐状态的取值空间为{B,E,M,S}。同时对隐状态的转移概率可以给出一些先验知识,B和M后面只能是M或者E,S和E后面只能是B或者S。而每个字就是模型中观测状态,取值空间为语料中的所有中文字。完成建模之后,使用语料进行训练可以分有监督训练和无监督训练。有监督训练即对语料进行标注,相当于根据经验得到了语料的所有隐状态信息,然后就可以用简单的计数法来对模型中的概率分布进行极大似然估计。无监督训练可以用Baum-Welch算法,同时优化隐状态序列和模型对应的概率分布。
因子图与马尔可夫逻辑网
马尔可夫逻辑网
一个马尔可夫逻辑网就是一个每个准则都有权重的一阶逻辑知识库,可看成是构建马尔可夫逻辑网络的模板。从概率的视角看,马尔可夫逻辑网提供一种简洁的语言来定义大型马尔可夫网,能灵活地、模块化地与大量知识合并;从一阶逻辑的视角看,马尔可夫逻辑网能健全地处理不确定性、容许有瑕疵甚至矛盾的知识库,降低脆弱性。有许多统计关系学习领域的重要任务,如集合分类、链接预测、链接聚合、社会网络建模和对象识别,都自然而然地成为运用马尔科夫逻辑网推理和学习的实例。
马尔可夫网(也叫马尔可夫随机场)是随机变量集$x=x_1,x_2,…,x_n$的联合分布模型,它由一个无向图G和一个势函数$\Psi_k$集合组成,每个随机变量是图上的节点,图的每个团在模型中都有一个势函数,势函数是一个非负实函数,它代表了相应的团的状态。马尔可夫网的联合分布如下:
其中$x$是团中随机变量的状态,Z也叫配分函数(态和),定义为$\sum{x\in X}\prodk\Psi_k(x)$。将马尔可夫网络中每个团的势状态的所有特征值加权后求和再取幂,就可方便地表示成对数线性模式
特征函数可以是表示状态的任何实函数。公式是势最直接的表示,其中每个团每个可能的状态都有一个对应的特征值 $f_j(x)$,它的权重是$w_j$,这种表示方法与团数量的幂相关。可是,我们可以自由地运用一些方法比如状态的逻辑函数等减少特征值数量,特别在团数量很大时能相比势函数方式提供一种更简洁的表示形式。马尔可夫逻辑网络就是利用了这一方式。

