最大似然概率
以测量校园里学生身高分布为例,分为男生和女生,分别抽取100个人。假设他们的身高是服从高斯分布的,但是这个分布的均值$\mu$和方差$\sigma^2$是未知的,我们要估计这两个参数,记作$\theta=[\mu,\sigma]^T$。
我们独立地按照概率密度$p(x|\theta)$抽取100个身高,组成样本集X,我们想通过样本集X来估计出未知参数$\theta$。其中的未知参数是$\theta = [\mu,\sigma]^T$。抽到的样本集是$X={x_1,x_2,…,x_N}$,其中$x_i$表示抽到第i个人的身高,N为抽到样本个数。
在$\theta$参数的情况下抽取得到样本集的概率,就是从分布是$p(x| \theta)$的总体样本中抽取到这100个样本的概率,也就是样本集X中各个样本的联合概率,用下式表示:
这里$L(\theta)$就是参数$\theta$相对于样本集的似然函数(likehood function)
那么$\theta$的最大似然估计量,记为:$\hat\theta = argmaxl(\theta)$
有时为了我便于分析与计算,定义对数似然函数,将连乘变成连加:
之后为求一个函数的最值,需要求导使得导数为0,那么解这个方程得到的$ \theta$就是了(前提是函数$L(\theta)$连续可微);如果$\theta$包含多个参数的向量,则求$L(\theta)$对所有参数的偏导数,n个未知的参数,就有n个方程,方程组的解就是似然函数的极值点。
求解最大似然函数估计值的一般步骤
(1)写出似然函数;
(2)对似然函数取对数,并整理;
(3)求导数,令导数为0,得到似然方程;
(4)解似然方程,得到的参数即为所求。
注意:参数只是对应了一个类别,也就是说男生,女生身高的问题,就是在已知这一群人都是男生的情况下,获得这个类别的参数,或者都是女生的情况下获得。如果两个类别混在一起,那么就是下面的EM估计了。
EM算法
EM出现的原因就是抽取的样本不知道是哪个分布抽取的。例如上例的最大似然,两种高斯分布的人(男生、女生)混在一块了,我们又不知道哪些人属于第一个高斯分布,哪些属于第二个,所以就没法估计这两个分布的参数。反过来,只有当我们对这两个分布的参数作出了准确的估计的时候,才能知道到底哪些人属于第一个分布,那些人属于第二个分布。所以这里就是说EM估计就是因为多了一个隐含变量(抽取得到的每个样本都不知道是从哪个分布抽取的)使得本来简单的可以求解的问题变复杂了。
简单的处理办法是先初始化隐含变量,然后估计出每个类别对应的分布参数。然后再根据这个分布参数去调整每个样本的隐含参数,依次迭代。其能迭代成功的原因在于我们可以证明似然函数是一个单调函数。
EM算法的推导
给定的训练样本是${x^{(1)},…,x^{(m)}}$,样例间独立,我们想找到每个样例隐含的类别z,能使得$p(x,z)$最大。$p(x,z)$的最大似然估计如下:
第一步是对极大似然取对数,第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求$\theta$一般比较困难,因为有隐藏变量z存在,但是一般确定了z后,求解就容易了,也就是说我们的目标是找到合适的$\theta$和z让$L(\theta)$最大。
EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化$l(\theta)$,我们可以不断地建立$l$的下界(E步),然后优化下界(M步)。
对于每一个样例i,让$Q_i$表示该样例隐含变量z的某种分布,$Q_i$满足的条件是$\sum_xQ_i(z) = 1, Q_i(z) \ge 0$。(如果z是连续性的,那么$Q_t$是概率密度函数,需要将求和符号换做积分符号)。比如要将班上学生聚类,假设隐藏变量z是身高,那么就是连续的高斯分布。如果按照隐藏变量是男女,那么就是伯努利分布了。
则似然公式如下:
看似最后只多了一个未知变量$Q_i(z^{(i)})$而已,实际上变到(3)式的时候公式由“和的对数”变为“对数的和”,这样求导就容易了。值得注意的是,(3)式变为了不等号,这就是Jensen不等式(就是对凹函数的公式: f(E[X]>=E[f(X)]))的大显神威的地方。
(1)到(2)比较直接,就是分子分母同乘以一个相等的函数。(2)到(3)利用了Jensen不等式,考虑到$\log(x)$是凹函数(二阶导数小于0),而且$\sum_{z^{(i)}}Q_i(z^{(i)})[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}]$就是$[p(x^{(i)},z^{(i)};\theta)/Q_i(z^{(i)})]$的期望。(依期望公式中的Lazy Statistician规则)
Lazy Statistician规则
设Y是随机变量X的函数,$Y=g(X)$(g是连续函数),那么:
(1) X是离散型随机变量,它的分布律为$P(X=xk) = p_k,k=1,2,…$。若$\sum{k=1}^{\infty}g(xk)p_k$绝对收敛,则有$E(Y) =E[g(X)] = \sum{k=1}^{\infty}g(x_k)p_k$
(2) X是连续型随机变量,它的概率密度为$f(x)$,若$\displaystyle\int^{\infty}{-\infty}{g(x)f(x)dx}$绝对收敛,则有$E(Y)= E[g(X)] =\displaystyle\int^{\infty}{-\infty}{g(x)f(x)dx}$
依据上述规则,上面的(2)式到(3)式的不等式可以写成:似然函数$L(\theta)>=J(z,Q)$,那么我们可以通过不断的最大化这个下界J,来使得$L(\theta)$不断提高,最终达到它的最大值。
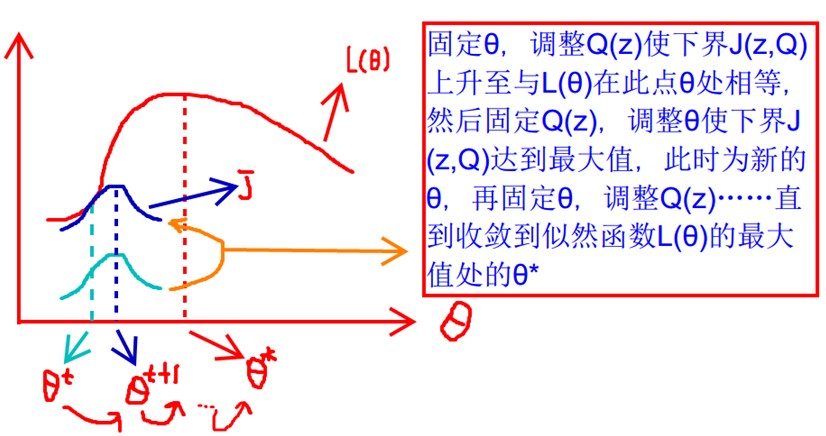
见上图,我们固定$\theta$,调整Q(z)使得下界$J(z,Q)$上升至与$L(\theta)$在此点$\theta$处相等(绿色曲线到蓝色曲线),然后固定$Q(z)$,调整$\theta$使下界$J(z,Q)$达到最大值($\theta^t$到$\theta^{t+1}$),然后再固定$\theta$,调整Q(z)…直到收敛到似然函数$L(\theta)$的最大值处的$\theta^{*}$。这里有两个问题:什么时候下界$J(z,Q)$与$L(\theta)$在此点$\theta$处相等?为什么一定会收敛?
这个过程可以看作是对$l(\theta)$求了下界。对于$Q_i$的选择,有多种可能,哪种更好?假设$\theta$已经给定,那么$l(\theta)$的值就决定于$Q_i(z^{(i)})$和$p(x^{(i)},z^{(i)})$了。我们可以通过调整这两个概率使下界不断上升,以逼近$l(\theta)$的真实值,那么什么时候算是调整好了呢?当不等式变成等式时,说明我们调整后的概率能够等价于$l(\theta)$了。按照这个思路,我们要找到等式成立的条件。根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,这里得到:
c为常数,不依赖于$z^{(i)}$。对此式子做进一步推导,我们知道$\sum_zQ_i(z^{(i)})=1$,那么也就有$\sum_z p(x^{(i)},z^{(i)};\theta) =c$(多个等式分子分母相加不变,这个认为每个样例的两个概率比值都是c),那么有下式:
至此,我们推出了在固定其他参数$\theta$后,$Q_i(z^{(i)})$的计算公式就是后验概率,解决了$Q_i(z^{(i)})$如何选择的问题。这一步就是E步,建立$l(\theta)$的下界。接下来的M步,就是给定$Q_i(z^{(i)})$后,调整$\theta$,去极大化$l(\theta)$的下界(在固定$Q_i(z^{(i)})$后,下界还可以调整的更大)。那么一般的EM算法步骤如下:
循环重复直到收敛{
(E步),对于每一个i,计算
(M步),计算
}
究竟怎么确保EM收敛?假定$\theta^{(t)}$和$\theta^{(t+1)}$是EM第t次和t+1次迭代后的结果。如果我们证明了$l(\theta^{(t)})\le l(\theta^{(t+1)})$,也就是说极大似然估计单调增加,那么最终我们会到达最大似然估计的最大值。
感性的说,因为下界不断提高,所以极大似然估计单调增加,那么最终我们会到达最大似然估计的最大值。理性分析的话,就会得到下面的式子:
EM算法另一种理解
坐标上升法(Coordinate ascent):
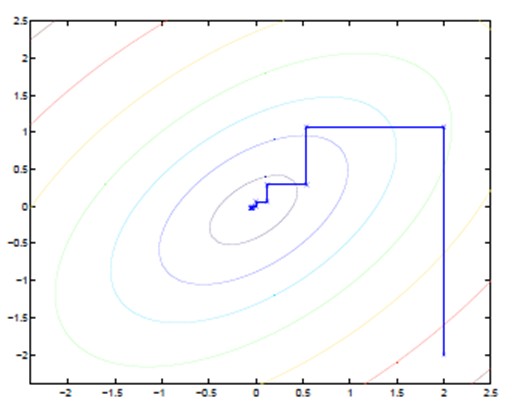
图中的直线式迭代优化的路径,可以看到每一步都会向最优值前进一步,而且前进路线是平行于坐标轴的,因为每一步只优化一个变量。
这类似在x-y坐标系中找一个曲线的极值,然而曲线函数不能直接求导,因此梯度下降的方法就不适用了。但固定一个变量后,另外一个可以通过求导得到,因此可以使用坐标上升法,一次固定一个变量,对另外的求极值,最后逐步逼近极值。对应到EM上,E步:固定$\theta$,优化Q;M步:固定Q,优化$\theta$;交替将极值推向最大。
EM的应用
EM算法有很多的应用,最广泛的就是GMM混合高斯模型、聚类、HMM等等。

